前回導き出したフレット間隔の謎の法則:iPhoneの計算機で出てきた数値は『1.059463094359295』でした。このブログでの表記は『1.0594』と省略して書くことにしましょう。
さてこのフレット間隔の謎の法則により、ギターの音が1フレットあがると、弦の振動数が1.0594大きくなることがわかりました。というわけで今回は、この1.0594という数字を使って、実際にギターのフレット位置を計算してゆきます。
音が1オクターブ上がった時、弦の振動数は2倍の大きさになり、弦の長さは1/2だけ短くなる事は前回書きました。つまり振動数と弦の長さは「反比例」の関係にあるわけです。なので音が1フレット上がった場合は、振動数が1.0594倍なり、弦の長さは1/1.0594になるという事です。
ちなみに今回作るファイヤーバードは弦の長さが628ミリのミディアムスケールでいきます(ギブソンではこれが標準的なサイズのようです)。開放弦で628ミリというわけです。ですから、1フレット目を押さえた時の弦の長さは628ミリに1/1.0594をかけた数……628を1.0594で割ればいいわけです。
628÷1.0594=592.7530
0フレットから1フレットまでの長さは、解放弦の長さからこれを引けばいいわけで、
628-592.7530=35.247
1フレット目の位置が約35.2ミリという事がわかりました! ばんざーい!
でも割ってから引くのってのが面倒くさいですね。628を1.0594で割るかわりに、(1−1/1.0594)をかける事にしましょう。こうすれば一発(?)で1フレット目までの長さが出せる(はず)です。
628×(1−1/1.0594)=35.2308
というわけで、1フレット目は約35・2ミリである事は間違いないようですね。さあこの調子で2フレットから先もバンバン計算して……え? 何? 一回目の計算と違うって? ……そうなんです。計算の途中で出てくる小数点以下をどうするかによって微妙に違ってきちゃうわけなんです。
円周率とかもそうですが、この手の数、小数点以下が延々と出てきちゃうような計算というのは、完璧に計算してピッタシの答えを出すことができません。ひとつだけの答えを求めるだけならいいのですが、ギターのフレット位置のように相対的なものを決める場合難しいです。計算上の数値は出せたとしてもそれをギターの指板という物体に書き写すとなるとどうすればいいのやら……。誤差の問題……というよりバランス問題とでもいえばいいのでしょうか? きっと理系の人なら上手な妥協のしかたを知っているのかもしれませんが、根っから文系の筆者には思いつきません。
そんな時、とても筆者向けのいい方法がある事を知りました。『図形から求める』という方法です。
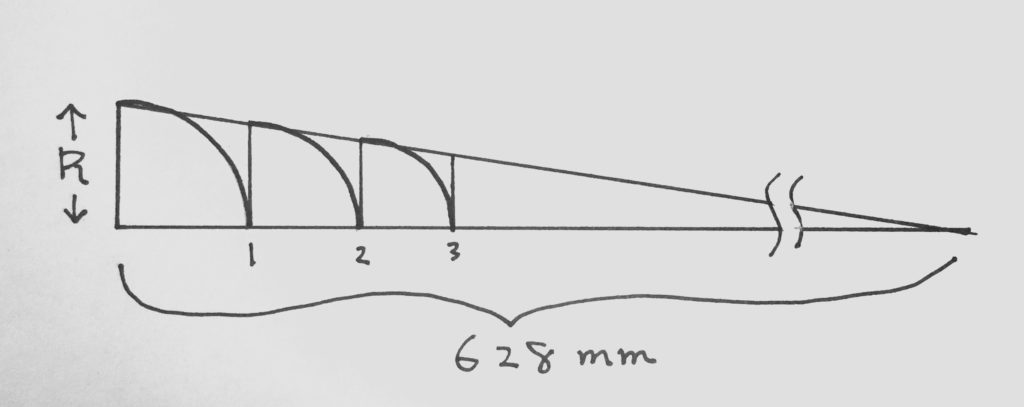
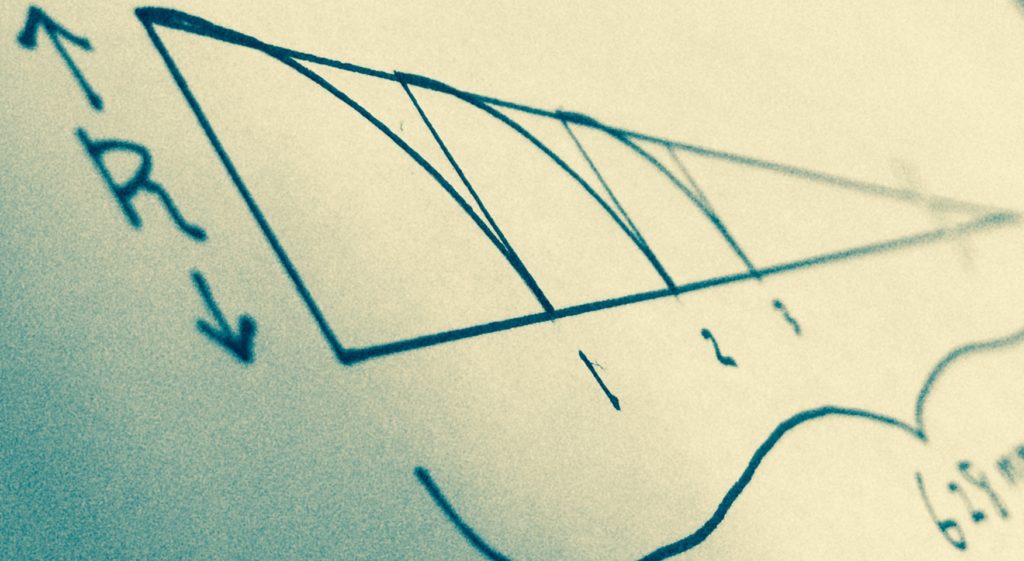
まず今回のギターのスケール628ミリの基準線を引き、左端をナットに見立て図のRに1フレット目までの長さの垂直線を立てます。さらにRの上端と基準線の右端を繋ぎ、細長い直角三角形を描きます。
このRの上端からコンパスを使って弧を描き、基準線と交わった点で、また垂直線を立てます。これを繰り返してゆくと……面倒な計算をしなくても、たちまち次のフレット位置がわかるというものです。
何と素晴らしい方法でしょう! ギター製作でコンパスを使うという意外さ! そして何より作業が楽しい! 一体誰が思いついたのでしょう。迷わずに今回はこの方法でゆこうと思いました! しかし……大きな問題があります。結果としては「こうなる」とわかった気がするものの、「なぜこうなるか?」が、いくら考えても全く理解できないのです……。
しかし……ここで止まってしまっては、ギター製作は進みません。この案件については自分にとっての大きな課題として残しつつ先へ進もうと思います。う〜ん、もやもやする……。