遅々として進まない自作ファイヤーバードですが、頭の中ではずっと進行中です。というのも以前に投稿した図形を使ったフレット計算方法の事をずっと考えていたわけです。そしてようやく、ふとした事からなんとなく理解できた気がしたのでここにメモしておくことにします。
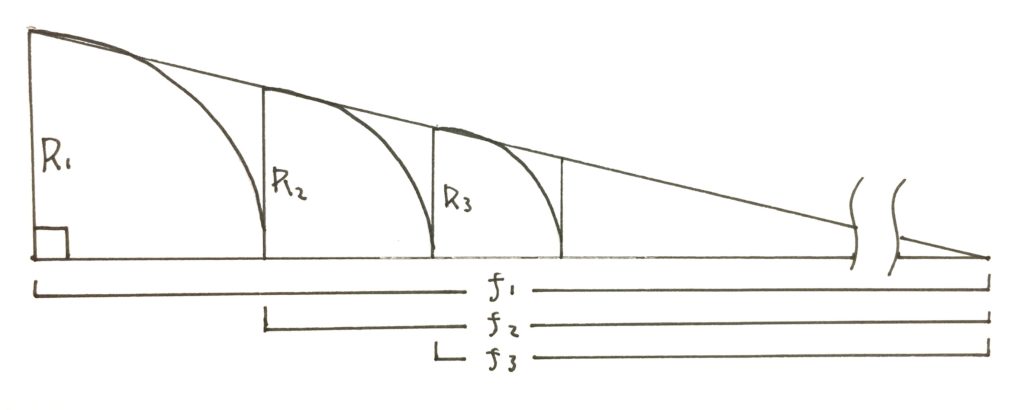
おさらいします。弦の長さf1を底辺にして、1フレット目の長さを垂直線R1とした直角三角形を作った時、Rの頂点からコンパスで弧を描き底辺と交わった点からさらに垂直線R2を立てる……という作業を繰り返してゆくと、2フレット目以降のフレットの幅が求められるという不思議な方法です。
実際にやってみると、どうやらその通りになるらしい事は判ったものの「一体なぜ?」という疑問だけが頭の隅に残りずっとモヤモヤしておりました。もしかしたら筆者の頭脳では理解できない複雑な理由なのか……? などとも考えました。
しかし、ある時(昨日の夕方)突然、以下の内容がひらめきました。
「この図は、いくつもの直角三角形が重なったものである」
「さらに、対となる垂直線Rと底辺Fの比は常に一定である」
フレットの幅を求める計算方法は前の投稿を参照していただくとしまして……1フレット目の幅は解放弦の長さに(1−0.94388=0.05612)をかけた長さ。さらに、2フレット目の幅は1フレットを押さえた時の弦の長さに同じく0.05612をかけた長さ。3フレット目の幅は2フレットを押さえた時の長さ×0.05612となります。
つまり、この直角三角形の垂直線Rと底辺Fの比は常に「0.05612」なのです。垂直線と底辺の比が同じ直角三角形の場合、底辺の直角ではない方の角の角度は常に一定ですから、全ての三角形を重ねると上記の図になるというわけです。
解ってしまえばとてもシンプルです。しかしとはいえ何もない所から思いつくものではありません。『それぞれのフレットの幅と、弦の長さの関係』に目をつけ、それを直角三角形にしてみる……といった感じで考えたのでしょうか。この方法を見つけた人はすごいです。とにもかくにも、これでようやくスッキリした気持ちで先へ進めそうです! やるぞ!

ちなみに、今回これを思いついた時に読んでいたのがグレッグ・イーガンの『シルトの梯子』でした。昨年暮れから読み始めたものの中々進まずまだ序盤で、さらに他のイーガン作品同様何が書いてあるか判らないことだらけであるにも関わらずとても引き込まれます。内容は別にギターのフレットの話でもなければ、三角関数の話でもないのですが、読んでいる途中になぜかふと思いついたのですから思考とは不思議なものですね。