ファイヤーバードの続きです。前回はネック材を切り出しました。そのままどんどん成形を進めたいところですが、平行して指板を作り始めることにします。

指板材にフレットの位置を決めて溝を彫るというこの工程。ギター工作ではなかなかの苦行とされてるようですね。しかし何事もやってみなければわかりません。恐れず進みましょう。(ギターワークスさんなど自作ギター専門店では、すでにフレット用の溝が彫られた指板が売っているのでてっとり早くいきたい場合は買っちゃうのもアリかもしれませんね)
さて今回は少し長くなりそうです。続きは以下で。
ギターのフレットを観察すると、高音のポジション(ギターのボディ方向)に向かうほど間隔が狭くなっているのがわかります。この「フレット間隔の謎の法則」によってギターという楽器が成立しているわけですが、一体どんなふうに決められているのでしょう?
今回は、自分のためのメモという意味もこめて、できるだけ簡潔に整理してみようと思います。
低い「ド」と高い「ド」のような関係をオクターブといいますが、オクターブがひとつ上がると、何と周波数がちょうどぴったり2倍になります。周波数……つまり空気を揺れて発生する波の数、これはギターの弦の振動に置き換えられるので「振動数」と呼ぶことにしましょう。この振動数は、まっすぐに張られた弦の長さをちょうど半分にすると、鳴らされる音は1オクターブ高い音となるわけです。ギターの場合は開放弦に対して12フレットが1オクターブ上と決まっていますので、ナットからブリッジまでの間のちょうど真ん中ピッタシが12フレットの位置となるわけです。
なるほどなるほど。意外とシンプルですね。さてさて問題はここから先なのです。
このオクターブとオクターブの間には、誰もが知っている12音階が存在します。(平均律については面倒臭いのでまた別の機会にしましょう)なので次は、指板上にこれらの音階の位置を探してゆくわけです。「12フレットの位置が決まったなら、その間を12等分すりゃいいんじゃねーの?」などと思ってしまいますが、それをやるととんでもなく音痴なギターができあがってしまいます。何故でしょう?
ここで再びオクターブの話に戻ります。先にも書いたように「オクターブがひとつ上がると弦の長さが半分」になります。ではそのまた上のオクターブとなるとどうなるか? 答えは簡単「そのまた半分」となるわけです。その先も同様に「そのまた半分」「そのまた半分」の繰り返し(まあギターの場合そんなに先までないのですが)。
つまり、音が高くなる程、弦の長さの変化は小さくなって、フレット間隔も狭くなってゆくことになります。グラフにすると右肩さがりの二次曲線となります。要するにフレット間隔は音が高くなるにつれ、あるルールに従ってちょっとづつ狭くなってゆくのです。このルールこそが冒頭に出てきた「フレット間隔の謎の法則」なのです。
というわけで12音階の話に戻ります。この「だんだん微妙に狭くなってゆく正しい12音階のフレット位置」を見つけるには、どうにかして「フレット間隔の謎の法則」の具体的な姿を探し出さなくてはなりません。唯一の手がかりは「オクターブあがると振動数はちょうど2倍」というキーワードです。
ここでとうとう、みんなの大嫌いな数式が登場してしまいます。避けては通れない道です。覚悟するしかありません。
まず、第1フレットを鳴らした振動数は、「0フレットで鳴らした振動数(f)」から比べて「謎の法則(N)」の分だけ上がるので、これを数式にすると、
f×N
さらに第2フレットは、そこにさらに「謎の法則(N)」分上がるので……、
f×N×N
これを繰り返してゆくと、第12フレットは……
f×N×N×N×N×N×N×N×N×N×N×N×N
「開放弦の振動数(f)」に「謎の法則(N)」を12回かけた値、つまりfかけるNの12乗ですね。
f×N^12
さらにこの第12フレットの振動数は開放弦のオクターブ上なので、振動数は開放弦のちょうど2倍となるわけで……
f×N^12=f×2
でもって、この式を整理します。fが消えて、左の12乗を右に持ってゆくと……、
N^12=2
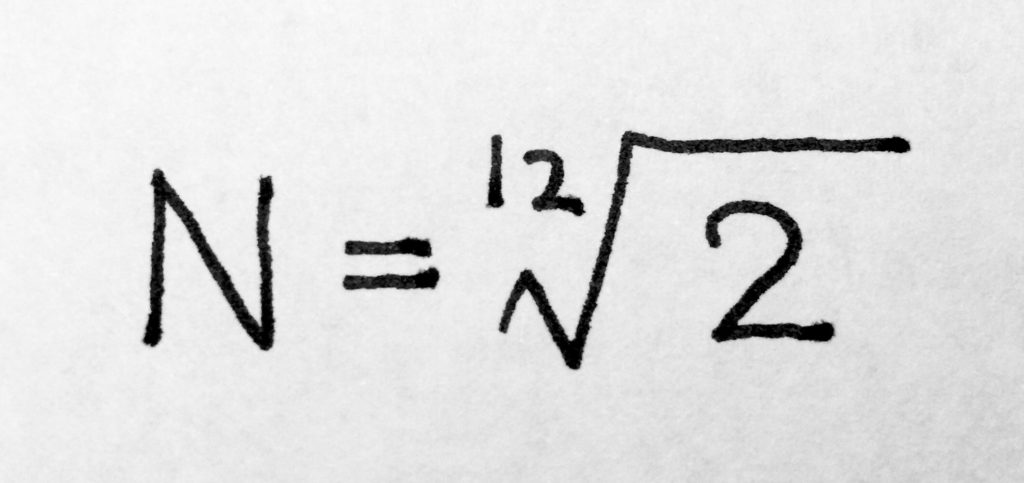
N=2の12乗根
12じょうこん……? これどうやって計算するんだっけ……? わからないので計算機を使っちゃいましょう。
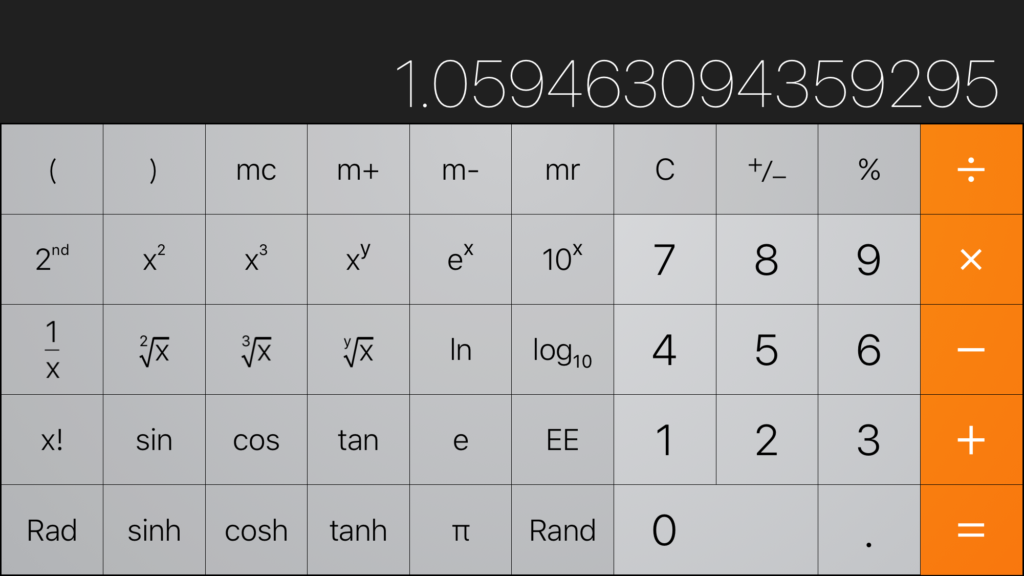
こんなん出ました。1.0594うんたらかんたら。そうです。この1.0594うんたらかんたらという数字こそが「フレット間隔の謎の法則」の正体なのです!
さて。長くなってしまいましたので、続きは次回にいたしましょう。うう〜疲れた……。